X-150 - A Micro Turbojet Engine

Watch me build my engine from scratch !

　
　 Back Next

The CRS Program

Picture

Description
CRS = Critical Rotational Speed. When the shaft is spinning we don't wish the system be resonant at any natural frequencies.  This can be done by limiting the rotational speed lower than system's lowest natural frequency.  We of course can utilize any commercial finite element codes to solve it, but they are large ,expensive and complicated not suitable for home builders. A special program like what we are doing might be quite nice.

We start the formulation by this 2D beam element. Only the first mode (bending mode) is important, so axial degree of freedom will not be considered.
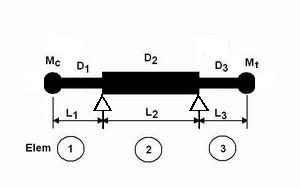Divide the whole shaft into three beam elements. Mass of compressor and turbine wheel indicated as Mc and Mt respectively.
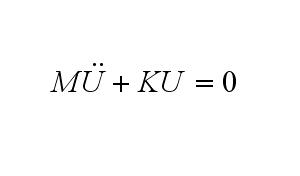Assembling each element's mass matrix and stiffness matrix, we get M and K. The free vibration problem now has the form shown left. We have 8 DOFs, two of which constrained. so the final size of U is 6 DOFs only. 6 DOF is complicated enough for hand calculation.
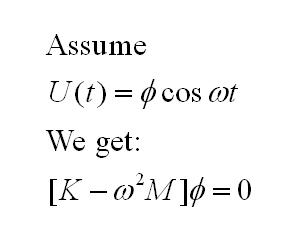To solve the system equation, we transform it into generalized form of eigenproblem.

 
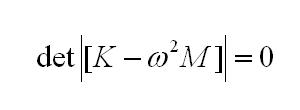Let the determinant of the system equation be zero we can  solve for lowest ω (unit = rad/sec). However this takes hand calculation and is extremely lengthy and difficult.

This is how we calculate the critical rotational speed. What we'll do is to use numerical methods such as Rayleigh-Ritz subspace iteration method or Generalized Jacobi method instead, to find the natural frequencies and mode shapes. If you are interested in these methods, please find them in many Finite Element textbooks.

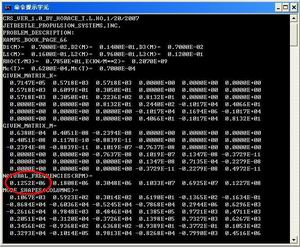Here is a sample of program output.

We reanalysis the natural frequency of Kamps' book page 66. Click to see larger picture.

it shows ours is 125,200 rpm and Kamps' 136,270 rpm. The maximum design speed was 105,000rpm so it is safe. It is very interesting that our result is the lower bound of Kamps'.  

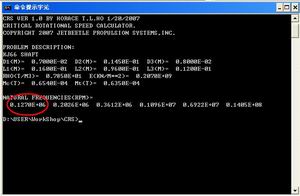Another sample of program output. Click to see larger picture.

KJ66 is a famous engine now we are able to check the critical rotational speed in just a minute. We minimize the program output for brevity. Our program shows 127Krpm, it is very reasonable because the max rpm of KJ66 was set at 117K rpm. 

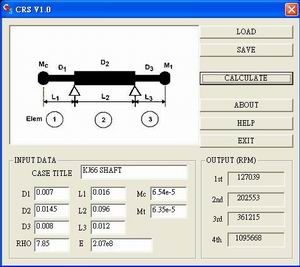This is our user interface looks like. A lot of coding works but finally done. We will extend this program to allow more shaft configurations, your help in funding us is highly appreciated.

We  successfully integrated Fortran and C++ so that the user interface and numerical core are seamlessly working together.  

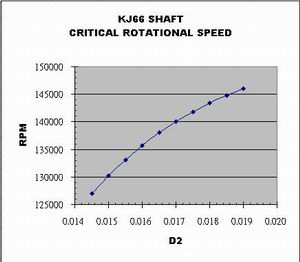Now we have a new toy to play around. Again the shaft being analyzed is KJ66, we choose D2 as parameter to study. We enter different D2 values starting from 0.0145, increments 0.0005 each time and collect the CRS output values, we get this chart. It shows that if we'd like kj66 to run at higher rpms and thus higher thrusts, we can change D2 to Φ0.017m or Φ17mm. Shaft tunnel must be changed too.  This program is of thousands of dollars of value ! Should I give it out for free ?
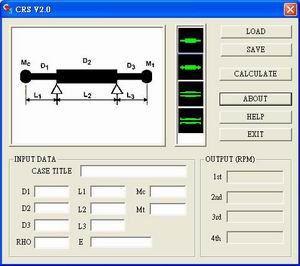CRS V2.0 is under development. This is probably our user interface will be looks like. As you can see the shafts available are more than one. A List box is shown in the middle so user can pick the shaft they want to do the analysis.